Fast Linear Projection with Circulant Matrices
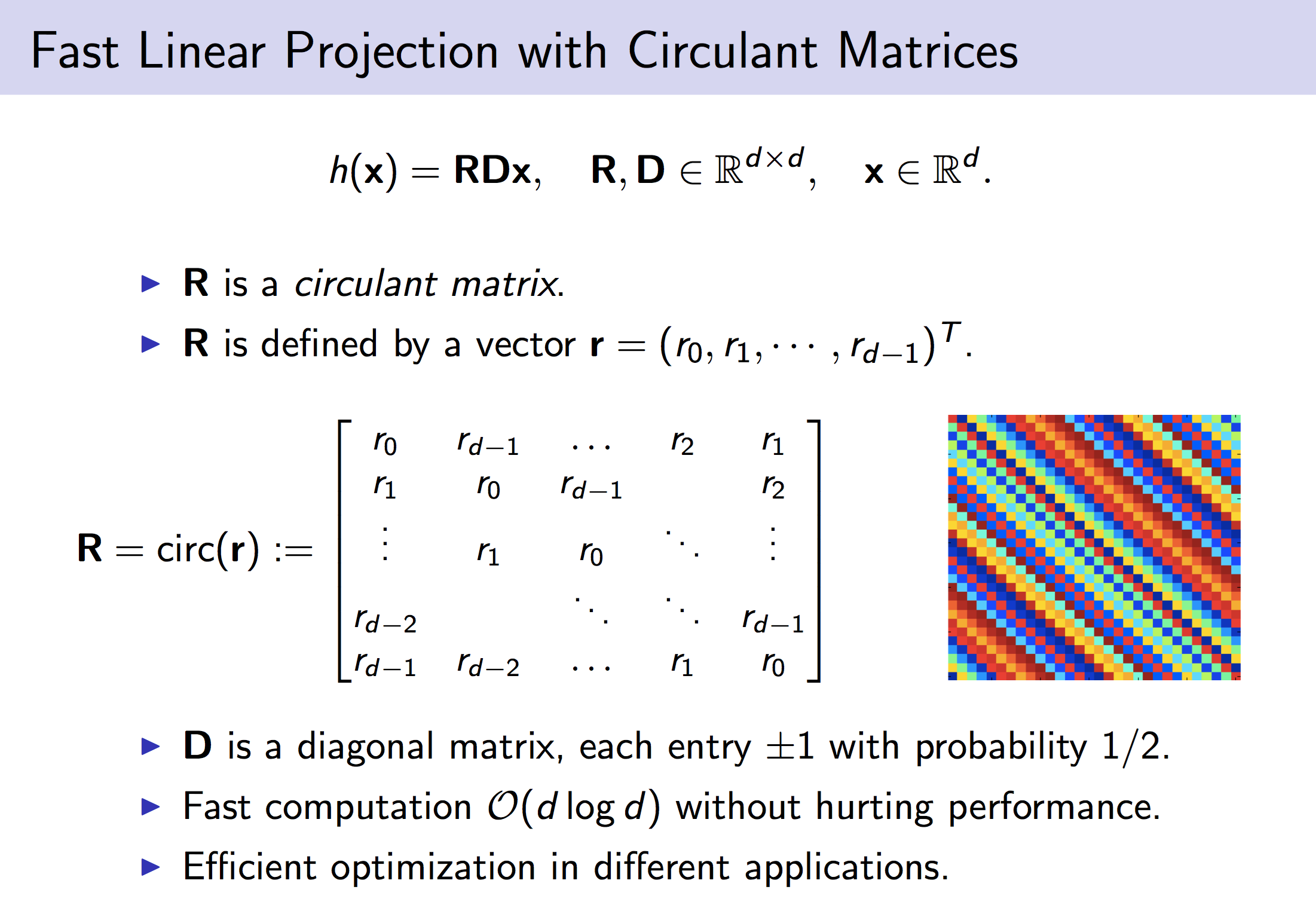
Circulant Binary Embedding
Binary embedding of high-dimensional data requires long codes to preserve the discriminative power of the input space. Traditional binary coding methods often suffer from very high computation and storage costs in such a scenario. To address this problem, we propose Circulant Binary Embedding (CBE) which generates binary codes by projecting the data with a circulant matrix. The circulant structure enables the use of Fast Fourier Transformation to speed up the computation. Compared to methods that use unstructured matrices, the proposed method improves the time complexity from O(d^2) to O(dlogd), and the space complexity from O(d^2) to O(d) where d is the input dimensionality. We also propose a novel time-frequency alternating optimization to learn data-dependent circulant projections, which alternatively minimizes the objective in original and Fourier domains. We show by extensive experiments that the proposed approach gives much better performance than the state-of-the-art approaches for fixed time, and provides much faster computation with no performance degradation for fixed number of bits.
Fast Neural Networks with Circulant Projections
The basic computation of a fully-connected neural network layer is a linear projection of the input signal followed by a non-linear transformation. The linear projection step consumes the bulk of the processing time and memory footprint. In this work, we propose to replace the conventional linear projection with the circulant projection. The circulant structure enables the use of the Fast Fourier Transform to speed up the computation. Considering a neural network layer with d input nodes, and d output nodes, this method improves the time complexity from O(d^2) to O(dlogd) and space complexity from O(d^2) to O(d). We further show that the gradient computation and optimization of the circulant projections can be performed very efficiently. Our experiments on three standard datasets show that the proposed approach achieves this significant gain in efficiency and storage with minimal loss of accuracy compared to neural networks with unstructured projections.
Compact Nonlinear Maps and Circulant Extensions
Kernel approximation via nonlinear random feature maps is widely used in speeding up kernel machines. There are two main challenges for the conventional kernel approximation methods. First, before performing kernel approximation, a good kernel has to be chosen. Picking a good kernel is a very challenging problem in itself. Second, high-dimensional maps are often required in order to achieve good performance. This leads to high computational cost in both generating the nonlinear maps, and in the subsequent learning and prediction process. In this work, we propose to optimize the nonlinear maps directly with respect to the classification objective in a data-dependent fashion. The proposed approach achieves kernel approximation and kernel learning in a joint framework. This leads to much more compact maps without hurting the performance. As a by-product, the same framework can also be used to achieve more compact kernel maps to approximate a known kernel. We also introduce Circulant Nonlinear Maps, which uses a circulant-structured projection matrix to speed up the nonlinear maps for high-dimensional data.
Fast Orthogonal Projection Based on Kronecker Product
We propose a family of structured matrices to speed up orthogonal projections for high-dimensional data commonly seen in computer vision applications. In this, a structured matrix is formed by the Kronecker product of a series of smaller orthogonal matrices. This achieves O(d log d) computational complexity and O(log d) space complexity for d-dimensional data, a drastic improvement over the standard unstructured projections whose computational and space complexities are both O(d^2). We also introduce an efficient learning procedure for optimizing such matrices in a data dependent fashion. We demonstrate the significant advantages of the proposed approach in solving the approximate nearest neighbor (ANN) image search problem with both binary embedding and quantization. Comprehensive experiments show that the proposed approach can achieve similar or better accuracy as the existing state-of-the-art but with significantly less time and memory.
Orthogonal Random Features
We present an intriguing discovery related to Random Fourier Features: in Gaussian kernel approximation, replacing the random Gaussian matrix by a properly scaled random orthogonal matrix significantly decreases kernel approximation error. We call this technique Orthogonal Random Features (ORF), and provide theoretical and empirical justification for this behavior. Motivated by this discovery, we further propose Structured Orthogonal Random Features (SORF), which uses a class of structured discrete orthogonal matrices to speed up the computation. The method reduces the time cost from O(d^2) to O(dlogd), where d is the data dimensionality, with almost no compromise in kernel approximation quality compared to ORF. Experiments on several datasets verify the effectiveness of ORF and SORF over the existing methods. We also provide discussions on using the same type of discrete orthogonal structure for a broader range of applications.
Publications
Felix X. Yu; Sanjiv Kumar; Yunchao Gong; Shih-Fu Chang. Circulant Binary Embedding ICML 2014 [PDF] [Slides] [arXiv] [GitHub] [Project]
Felix X. Yu, Aditya Bhaskara, Sanjiv Kumar, Yunchao Gong, Shih-Fu Chang On binary embedding using circulant matrices
[arXiv:1511.06480]
Yu Cheng*, Felix X. Yu*, Rogerio Feris, Sanjiv Kumar, Alok Choudhary, Shih-Fu Chang (* equal contribution) An exploration of parameter redundancy in deep networks with circulant projections ICCV 2015 (acceptance rate 20%) [PDF] [arXiv] [Project]
Felix X. Yu; Sanjiv Kumar; Henry Rowley; Shih-Fu Chang. Compact Nonlinear Map and Circulant Extensions
[arXiv:1503.03893]
Xu Zhang, Felix X. Yu, Ruiqi Guo, Sanjiv Kumar, Shengjin Wang, Shih-Fu Chang Fast orthogonal projection based on Kronecker product ICCV 2015 (acceptance rate 20%) [PDF] [GitHub] [Project]
Felix X. Yu, Ananda Theertha Suresh, Krzysztof Choromanski, Daniel Holtmann-Rice, Sanjiv Kumar Orthogonal random features NIPS 2016 oral (full-length) (acceptance rate 1.8%) [arXiv]
